
Here, a strong relationship does exist between the two data elements, and it has a positive sense. There are important differences in this case, however, compared to the previous. Like the previous example, we are challenged by a single outlying value. Suppose that a single data entry error occurs (let's say a shifting of the decimal point ), and the data elements originally shown in Figure 1 appear now as in Figure 5. Let’s turn now to a second example of correlation gone awry. Now, the single outlying value induces a correlation value of 0.58 – certainly high enough to suggest a strong relationship where, in fact, there really is none. In Figure 3, we saw that the correlation was approximately zero for the properly aligned data. The result is shown in Figure 4, with the outlying value clearly marked in the scatter plot.
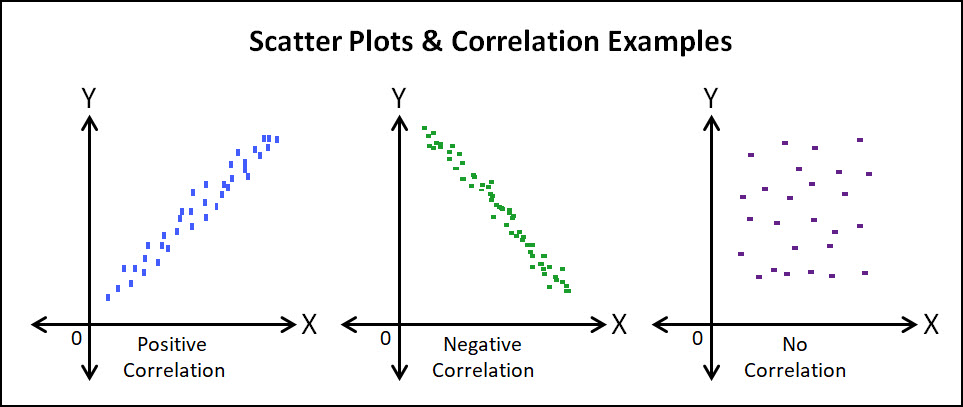
The misalignment occurs in only a single row of data, and large values from adjacent columns are inserted into the wrong slots. Suppose further that, in loading the data set which includes these two elements, a column alignment problem occurs. The scatter plot of these elements looks like the “shotgun blast” depicted in Figure 3. What could possibly go wrong? As it turns out, plenty can go wrong.Īs a first example of what can go wrong, suppose you have two data elements that are uncorrelated. For instance, referring again to Figure 1, the positive correlation value tells us that income increases with age – and the scatter plot confirms it. In addition, the sign (+ or -) of the correlation indicates the “sense” of the relationship. Sounds ideal, doesn’t it? With a single number, we get a quantitative measure of whether or not two data elements, such as age and income, are related, and to what degree. The more tightly the data hugs the best-fit line, the larger the magnitude of the correlation – that is, the closer it will be to either -1 or +1. A line of best fit that is flat, or nearly so, has a correlation near zero, as shown in Figure 3. A best-fit line slanting downward to the right, depicted in Figure 2, indicates a negative correlation. A positive correlation is associated with a best-fit line that slants upward to the right, like that in Figure 1. By design, the correlation value can range from -1 to +1. (“R” or “r” is the traditional letter designation for correlation).Ĭorrelation is a statistical measure, and it indicates how well, or poorly, a straight line conforms to a pair of data elements. Finally, the legend on the plot reports the correlation measure, r=0.98. Note also the dotted line in the plot that is the “best fit” of a straight line to the age-income data. In this scatter plot, each dot represents a different customer. My goal is to help you avoid the usual pitfalls, so that you can use correlation and scatter plots effectively in your own work.Ĭonsider the graph of income versus age that is shown in Figure 1. As we’ll soon see, there are good, bad, and ugly things that can happen when you apply a purely computational method like correlation. Or, you might compute a number that is the correlation between these two customer demographics. For instance, you might want to view the relationship between the age and income of your customers as a scatter plot. These tools are fundamental for gauging the relationship (if any) between pairs of data elements. We will tackle two, intertwined tools/topics this time: correlation and scatter plots. In this article, I continue the “Nuts and Bolts of Data Mining” series. Nuts and Bolts of Data Mining: Correlation & Scatter Plots


 0 kommentar(er)
0 kommentar(er)
